serie_II_2.mw
Serie 1 (Suter)
Funktion mass zur berechnung der Atommasse in MeV/c^2
| > |
# Umrechnung in MeV/c^2 |
| > |
faktor := 5.6096E29; #/2.99792458E8; #??? |
| > |
m_P:=1.67262158E-27 * faktor; |
| > |
m_N:=1.67492716E-27 * faktor; |
| > |
m_e:=9.10938188E-31 * faktor; |
| > |
m_H:=m_P+m_e; # nicht ganz, aber beinahe |
| > |
if( type(Z,even) and type(A-Z,even) ) then |
| > |
if( type(Z,odd) and type(A-Z,odd) ) then |
| > |
# Energie berechnen (in MeV/c^2) |
| > |
Z*m_H + (A-Z) * m_N - a_V * A + a_S * A^(2/3) + a_C * Z^2 * A^(-1/3) + a_A * (Z-A/2)^2/A + rho * a_P * A^(-1/2); |
Warning, `faktor` is implicitly declared local to procedure `mass`
Warning, `m_P` is implicitly declared local to procedure `mass`
Warning, `m_N` is implicitly declared local to procedure `mass`
Warning, `m_e` is implicitly declared local to procedure `mass`
Warning, `m_H` is implicitly declared local to procedure `mass`
Warning, `a_V` is implicitly declared local to procedure `mass`
Warning, `a_S` is implicitly declared local to procedure `mass`
Warning, `a_C` is implicitly declared local to procedure `mass`
Warning, `a_A` is implicitly declared local to procedure `mass`
Warning, `a_P` is implicitly declared local to procedure `mass`
Warning, `rho` is implicitly declared local to procedure `mass`

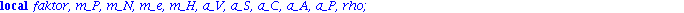













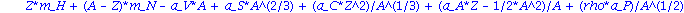

| > |
# Testen (Werte in MeV) |
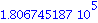
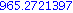
| > |
# Die Ergebnisse stimmen mit der Nuklid-Tabelle überein jedoch sind die Werte in MeV??? |
| > |
evalf( mass(235,92) - ( mass(95,38) + mass(140,54) ) ); |
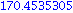
| > |
# Vergleich mit Tabelle (Werte in MeV) |
| > |
( 235.0439231 - ( 94.9193582 + 139.9216357 ) ) * 9.3149E2; |
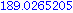
| > |
# Weiter Zerfall (Werte in MeV) |
| > |
# Sr-95->(Beta-) Y-95 ->(Beta-) Zr-95 ->(Beta-) Nb-95 ->(Beta-) Mo-95 (stable) 94.9058415 amu |
| > |
# Xe-140 ->(Beta-) Cs-140 ->(Beta-) Ba-140 ->(Beta-) La-140 ->(Beta-) Ce-140 (stable) 139.9054340 amu |
| > |
U_Zerfall := ( 235.0439231 - ( 94.9058415 + 139.9054340 ) ) * 9.3149E2; |
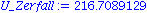
| > |
# in einem Gramm angereichertes Uran sind wieviele U-235 Atome? |
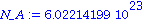
| > |
U_Energie_MeV := 1 * 0.03 * N_A * U_Zerfall; |
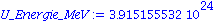
| > |
U_Energie_GJJ := U_Energie_MeV * 1.6022E-13 * 1E-9; |
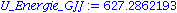
| > |
evalf((3 * Pi*1E7) / U_Energie_GJ)/1000; |
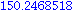
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()